Foreground publications during the project:

- B. Molnár, R. Sumi, M. Ercsey-Ravasz, "A CNN SAT-solver robust to noise", CNNA2014 Proc. of the 14th IEEE Int. Conf. on Cellular Nanoscale Networks and their Applications, accepted, Notre Dame, IN, USA (2014)

- R. Sumi, B. Molnar, M. Ercsey-Ravasz, "Robust optimization with transiently chaotic dynamical systems", EPL, 2014, accepted.

The heavily connected brain - Cortical high-density counterstream architectures

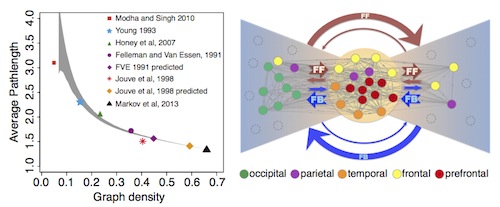
Background.The cerebral cortex is divisible into many individual areas, each exhibiting distinct connectivity profiles, architecture, and physiological characteristics. Interactions among cortical areas underlie higher sensory, motor, and cognitive functions. Graph theory provides an important framework for understanding network properties of the interareal weighted and directed connectivity matrix reported in recent studies.Density and topology of the cortical graph. Figure (Left) The 66% density of the cortical matrix (black triangle) is considerably greater than in previous reports (colored points) and is inconsistent with a small-world network. (Right) A bow-tie representation of the high-density cortical matrix. The high-efficiency cortical core has defined relations with the cortical periphery in the two fans. Advances. We derive an exponential distance rule that predicts many binary and weighted features of the cortical network, including efficiency of information transfer, the high specificity of long-distance compared to short-distance connections, wire length minimization, and the existence of a highly interconnected cortical core. We propose a bow-tie representation of the cortex, which combines these features with hierarchical processing. Outlook. The exponential distance rule has important implications for understanding scaling properties of the cortex and developing future large-scale dynamic models of the cortex.

The Exponential Distance Rule of the Brain

Recent advances in neuroscience have engendered interest in large-scale brain networks. Using a consistent database of cortico-cortical connectivity, generated from hemisphere-wide, retrograde tracing experiments in the macaque, we analyzed interareal weights and distances to reveal an important organizational principle of brain connectivity. Using appropriate graph theoretical measures, we show that although very dense (66%), the interareal network has strong structural specificity. Connection weights exhibit a heavy-tailed lognormal distribution spanning five orders of magnitude and conform to a distance rule reflecting exponential decay with interareal separation. A single-parameter random graph model based on this rule predicts numerous features of the cortical network: (1) the existence of a network core and the distribution of cliques, (2) global and local binary properties, (3) global and local weight-based communication efficiencies modeled as network conductance, and (4) overall wire-length minimization. These findings underscore the importance of distance and weight-based heterogeneity in cortical architecture and processing.

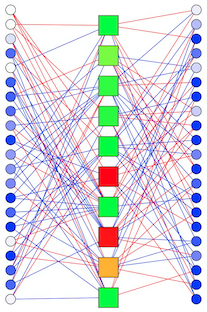
Asymmetric CNN without local traps for solving SAT problems

We present a deterministic continuous-time recurrent neural network similar to CNN models, which can solve Boolean satisfiability ($k$-SAT) problems without getting trapped in non-solution fixed points. The model can be implemented by analog circuits, in which case the algorithm would take a single operation: the template (connection weights) is set by the $k$-SAT instance and starting from any initial condition the system converges to a solution. We prove that there is a one-to-one correspondence between the stable fixed points of the model and the $k$-SAT solutions and present numerical evidence that limit cycles may also be avoided by appropriately choosing the parameters of the model.

- B. Molnár, Z. Toroczkai, M. Ercsey-Ravasz, CNNA2012 Proc. of the 13th IEEE Int. Conf. on Cellular Nanoscale Networks and their Applications, Torino, Italy (2012) doi:10.1109/CNNA.2012.6331411

The Chaos Within Sudoku

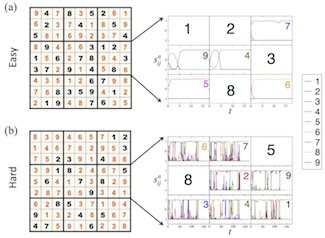
The mathematical structure of Sudoku puzzles is akin to hard constraint satisfaction problems lying at the basis of many applications, including protein folding and the ground-state problem of glassy spin systems. Via an exact mapping of Sudoku into a deterministic, continuous-time dynamical system, here we show that the difficulty of Sudoku translates into transient chaotic behavior exhibited by this system. We also show that the escape rate κ, an invariant of transient chaos, provides a scalar measure of the puzzle’s hardness that correlates well with human difficulty ratings. Accordingly, η=-log₁₀ (κ) can be used to define a ‘‘Richter’’-type scale for puzzle hardness, with easy puzzles having 0 < η ≤ 1, medium ones 1 < η ≤ 2, hard with 2 < η ≤ 3 and ultra-hard with η > 3. To our best knowledge, there are no known puzzles with η > 4.

Turbulent Computation

Boolean satisfiability (k-SAT) is one of the most studied optimization problems, as an efficient (that is, polynomial-time) solution to k-SAT (for k > 2) implies efficient solutions to a large number of hard optimization problems. Here we propose a mapping of k-SAT into a deterministic continuous-time dynamical system with a unique correspondence between its attractors and the k-SAT solution clusters. We show that beyond a constraint density threshold, the analog trajectories become transiently chaotic, and the boundaries between the basins of attraction of the solution clusters become fractal, signalling the appearance of optimization hardness. Analytical arguments and simulations indicate that the system always finds solutions for satisfiable formulae even in the frozen regimes of random 3-SAT and of locked occupation problems (considered among the hardest algorithmic benchmarks), a property partly due to the system's hyperbolic character. The system finds solutions in polynomial continuous time, however, at the expense of exponential fluctuations in its energy function.

Dr. Mária Ercsey-Ravasz

After obtaining Ph.D. in Physics and Information Technology, Dr. Ercsey-Ravasz have spent 3 years as a postdoctoral researcher at the University of Notre Dame, IN, USA. She returned to Romania to the Babes-Bolyai University in September 2011. She has started this Marie Curie Fellowship in May 2012.